The sum of consecutive squares formula

March 14, 2012

The sum of consecutive squares formula

Filed under: mathematics — ckrao @ 10:26 pm

This post shows two ways of seeing why the following sum of consecutive squares is true.

$\displaystyle 1^2 + 2^2 + 3^2 + \ldots + n^2 = \frac{n(n+1)(2n+1)}{6}$

The first way involves writing the numbers $1$ to $n$ in an equilateral triangle, where the $n$ th row consists of $n$ $n$ s. The sum of the numbers in such a triangle is $1.1 + 2.2 + \ldots + n.n$ which is what we wish to find.

We then consider the same triangle rotated by 120, then 240 degrees. This gives us three triangles, illustrated here in the case $n = 4$ .

Something magical happens when we add the corresponding entries of each triangle – we get the same number $(2n+1)$ everywhere!

The reason for this is that when one goes from an entry to an adjacent one (either left-right or diagonally), in one triangle the number increases by 1, in another it decreases by 1 and in the third it remains the same. Overall the sum of the three corresponding entries in each triangle is unaltered. This can be made rigorous by using coordinates (an exercise for the interested reader!).

Hence three times the sum of the numbers in each original triangle is $(2n+1)$ times the number of entries in the triangle: $1 + 2 + \ldots + n$ .

In other words,

$\displaystyle 1^2 + 2^2 + \ldots + n^2 = \frac{(2n+1)(1 + 2 + \ldots + n)}{3} = \frac{n(n+1)(2n+1)}{6},$

as desired.

The second way of seeing why the sum is true (that can be made into a rigorous proof) is to show that 6 times the sum is $n(n+1)(2n+1)$ . We consider six pyramids where the $n$ th level (counting from the top) consists of an $n\times n$ array of unit cubes. This is photographed here (while I visited this awesome place in Dresden, Germany) in the case $n=3$ .

These pyramids can then be joined together to form a rectangular box of dimension $n \times (n+1) \times (2n+1)$ as required.

Layer by layer, this appears as follows, where each pyramid is shown in a different colour.

To show that this was no fluke, here is the corresponding illustration of the 4x4x4 case, which should demonstrate how the above can be generalised.

Comments (8)

8 Comments »

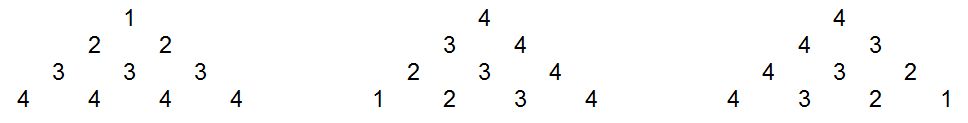
Excellent! Your final equation in the first method seems to be missing a factor of 3 on the left-hand side.

Comment by HT Goodwill — February 2, 2016 @ 5:13 pm | Reply
- Thanks for the correction! Now fixed.
  
  Comment by ckrao — February 4, 2016 @ 9:51 am | Reply
[…] $$sum_{k=1}^nk^2=frac16n(n+1)(2n+1)$$ has a geometric proof (scroll down just a bit til you see the wooden blocks) involving six copies of a 3D representation […]

Pingback by Geometric interpretation for sum of fourth powers - MathHub — April 5, 2016 @ 2:21 am | Reply
Thank You!

Comment by Phil — October 1, 2016 @ 10:21 pm | Reply
where is the place in Dresden?

Comment by Turgay Çoruhlu — September 17, 2017 @ 11:37 am | Reply
- I see the link has changed – now updated. See http://www.erlebnisland-mathematik.de/en/portfolio/beweise-ohne-worte-summe-der-quadratzahlen/
  
  Comment by ckrao — September 26, 2017 @ 11:27 am | Reply
Thank you, for this information
The blog is very informative. looking forward to reading more from you thank you
squares upto 50

Comment by shiva — June 12, 2021 @ 5:33 am | Reply
[…] n∑k=1k2=16n(n+1)(2n+1) has a geometric proof (scroll down just a bit til you see the wooden blocks) involving six copies of a 3D representation […]

Pingback by Geometric interpretation for sum of fourth powers – Math Solution — March 3, 2022 @ 12:53 am | Reply