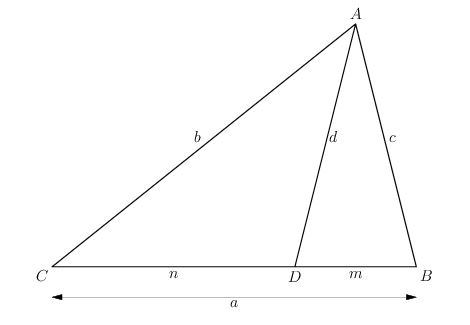
Forms of Stewart’s theorem

May 17, 2014

Forms of Stewart’s theorem

Filed under: mathematics — ckrao @ 10:41 am

Stewart’s theorem finds the length of a cevian $d=AD$ in terms of the side lengths of the triangle $ABC$ and the lengths $m, n$ into which point $D$ on $BC$ divides that side. Here are some forms of the same formula.

1. The most common form we see is

$\displaystyle b^2 m + c^2 n = a(d^2 + mn) \quad \Rightarrow \quad d^2 = \frac{b^2m + c^2n}{a} - mn.\quad\quad(1)$

An easy-to remember form of this is rewriting the above as $man + dad = bmb + cnc$ (a man and his dad hid a bomb in the sink!). This can be proved by applying the cosine rule to triangles ACD and then ABC:

$\begin{aligned} d^2 &= AD^2\\ &= AC^2 + CD^2 - 2AC.CD\cos \angle DCA\\ &= AC^2 + CD^2 - 2AC.CD \cos \angle BCA\\ &= AC^2 + CD^2 - 2AC.CD \frac{CA^2 + CB^2 - AB^2}{2CA.CB}\\ &= b^2 + n^2 - 2bn \frac{b^2 + a^2 - c^2}{2ba}\\ &= b^2 + n^2 - n \frac{b^2 + a^2 - c^2}{a}\\ &= \frac{b^2(m+n) - n(b^2 + a^2 - c^2)}{a} + n^2\\ &= \frac{b^2 m + c^2n}{a} + n^2 - \frac{na^2}{a}\\ &= \frac{b^2 m + c^2n}{a} + n(n-a)\\ &= \frac{b^2 m + c^2n}{a} - mn.\\ \end{aligned}$

2. If $D$ divides the side $BC$ in the ratio $BD:DC = r:s$ ,

$\displaystyle d^2 = \frac{rb^2 + sc^2}{r+s} - \frac{rsa^2}{(r+s)^2} = \frac{r^2b^2 + s^2c^2 + rs(b^2 + c^2 - a^2)}{(r+s)^2} .\quad\quad(2)$

3. Similar to (2) but substituting $\displaystyle \lambda = r/(r+s) = BD:BC$ ,

$\displaystyle d^2 = \lambda b^2 + (1-\lambda)c^2 - \lambda(1-\lambda)a^2.\quad\quad(3)$

This and the previous form are conveniently proved using vectors. Writing the vector $\mathbf{AD} = \lambda \mathbf{AC} + (1-\lambda) \mathbf{AB}$ ,

$\begin{aligned} d^2 &= \mathbf{AD}. \mathbf{AD}\\ &= \left(\lambda \mathbf{AC} + (1-\lambda) \mathbf{AB}\right).\left(\lambda \mathbf{AC} + (1-\lambda) \mathbf{AB}\right)\\ &= \lambda^2 \mathbf{AC}.\mathbf{AC} + (1-\lambda)^2 \mathbf{AB}.\mathbf{AB} + 2\lambda(1-\lambda)\mathbf{AB}.\mathbf{AC}\\ &= \lambda^2 b^2 + (1-\lambda)^2 c^2 + \lambda(1-\lambda)\left(b^2 + c^2 - a^2\right)\\ &= b^2(\lambda^2 + \lambda(1-\lambda)) + c^2((1-\lambda)^2 + \lambda(1-\lambda)) - a^2\lambda(1-\lambda)\\ &= \lambda b^2 + (1-\lambda)c^2 - \lambda(1-\lambda)a^2. \end{aligned}$

Note that this is valid for any real $\lambda$ , so $D$ may lie beyond segment $BC$ .

4. Writing (3) as a quadratic in $\lambda$ :

$\displaystyle d^2 = \lambda^2 a^2 + \lambda(c^2-b^2 -a^2) + b^2.\quad\quad(4)$

5. A symmetric form [1], where the following distances are taken as directed segments ( $CD = -DC$ etc.)

$\displaystyle \frac{BA^2}{BC.BD} + \frac{CA^2}{CB.CD} + \frac{DA^2}{DB.DC} = 1\quad\quad(5)$

Note that this is equivalent to $BA^2 . CD + CA^2 . DB = DA^2.CB + CD.DB.CB = CB(DA^2 + CD.DB)$ which is (1).

Here are a few special cases of this formula applying form (3).

$D = C$ (i.e. $\lambda = 1)$ : $d^2 = b^2$

$D$ is the midpoint of $BC$ ( $\lambda = 1/2$ ): $\displaystyle d^2 = b^2/2 + c^2/2 - a^2/4$ or $\displaystyle b^2 + c^2 = 2(d^2 + (a/2)^2)$ (Apollonius’ theorem)

$D$ is a third of the way along $CB$ (closer to $C$ ) ( $\lambda = 2/3$ ): $\displaystyle d^2 = 2b^2/3 + c^2/3 - 2a^2/9$

$AD$ is the internal angle bisector of $\angle BAC$ ( $\lambda = c/(b+c)$ ):

$\begin{aligned} d^2 &= cb^2/(b+c) + bc^2/(b+c) - bca^2/(b+c)^2\\ &= bc\left[\frac{b}{b+c} + \frac{c}{b+c}- \left(\frac{a}{b+c}\right)^2\right]\\ &= bc\left[1 - \left(\frac{a}{b+c}\right)^2\right]\\ &= bc - mn. \end{aligned}$

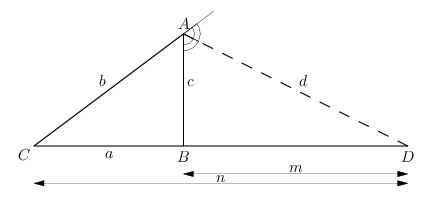
$AD$ is the external angle bisector of $\angle BAC$ (assume $b > c$ so $\lambda = -c/(b-c)$ ):

$\begin{aligned} d^2 &= \frac{-c}{b-c} b^2 + \frac{b}{b-c}c^2 + \frac{bc}{(b-c)^2}a^2\\ &= bc\left[\frac{-b}{b-c} + \frac{c}{b-c}+ \left(\frac{a}{b-c}\right)^2\right]\\ &= bc\left[ \left(\frac{a}{b-c}\right)^2 - 1\right]\\ &= mn - bc. \end{aligned}$

Reference

[1] Darij Grinberg – Unpublished Notes – Geometry

Leave a Comment »

No comments yet.

RSS feed for comments on this post. TrackBack URI

Chaitanya's Random Pages

May 17, 2014